ବିବିଧ ପ୍ରଶ୍ନ ୪୩
- $A B C$ ଏକ ସମବାହୁ ତ୍ରିଭୁଜ ଯାହାକୁ କେନ୍ଦ୍ର $O$ ଥିବା ଏକ ବୃତ୍ତ ମଧ୍ୟରେ ଅଙ୍କିତ ହୋଇଛି।
ପରିମାଣ I : OD ର ମାନ
ପରିମାଣ II : BD ର ମାନ
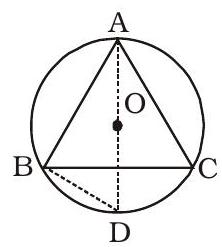
(1) ପରିମାଣ I $>$ ପରିମାଣ II (2) ପରିମାଣ I < ପରିମାଣ II
(3) ପରିମାଣ I $\leq$ ପରିମାଣ II
(4) ପରିମାଣ I $\geq$ ପରିମାଣ II
(5) ପରିମାଣ I = ପରିମାଣ II କିମ୍ବା କୌଣସି ସମ୍ପର୍କ ନାହିଁ।
Show Answer
ସଠିକ ଉତ୍ତର: 43. (5)
ସମାଧାନ:
- (5)
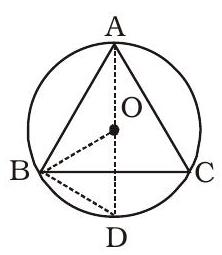
$\angle \mathrm{ABD}=90^{\circ}[\because \mathrm{AD}$ ବ୍ୟାସ ଅଟେ $]$
$\angle \mathrm{BDA}=\angle \mathrm{BCA}=60^{\circ}$
[ସମାନ ଚାପ ଦ୍ୱାରା ଅଙ୍କିତ କୋଣ]
$\therefore$ $\triangle \mathrm{BOD}$ ରେ,
$\angle \mathrm{OBD}=\angle \mathrm{ODB}=60^{\circ}$
$[\because \mathrm{OB}=\mathrm{OD}]$
$=\angle \mathrm{BOD}=60^{\circ}$ $\Rightarrow$ $\triangle \mathrm{BOD}$ ଏକ ସମବାହୁ ତ୍ରିଭୁଜ।
$\therefore \mathrm{OD}=\mathrm{BD}$।
ଅନ୍ୟ ଉପାୟ:
ବ୍ୟାସ $\mathrm{AD}$ କୋଣ $\angle \mathrm{BAC}$ କୁ ଦୁଇଭାଗ କରିବ $\Rightarrow$ $\angle \mathrm{BAD}=30^{\circ}$
$\triangle \mathrm{BAD}$ ରେ,
$\angle \mathrm{ABD}=90^{\circ}$
$\angle \mathrm{BAD}=30^{\circ}$
$[\because$ AD ବ୍ୟାସ ଅଟେ]
$\Rightarrow \angle \mathrm{BDA}=60^{\circ}$
$\Rightarrow \mathrm{BD}=\frac{1}{2} \mathrm{AD}=\mathrm{OD}$।



